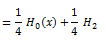Polinomios de Hermite

Los polinomios de Hermite

aparecen por primera vez, a raíz de la resolución del problema del oscilador armónico unidimensional en Mecánica Cuántica.

Están definidos en toda la recta real, es decir, su dominio será:

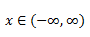
Por lo tanto, la función peso (w(x) recordemos) en el producto interno deberá menguar más rápido que |x|^n, para garantizar que la norma de los vectores en este espacio vectorial sea finita. La función mas sencilla que cumple estos requisitos es:

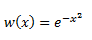
Entonces, el producto interno antes mencionado, entre polinomios de Hermite se puede definir como:

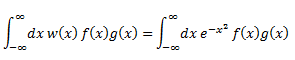
**Nota**: Nada más que hemos sustituido w(x) en la ecuación por la función que habíamos determinado anteriormente.

Existe una fórmula de Rodrigues para los polinomios de Hermite:

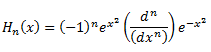
De tal forma que los primeros cinco polinomios serán los siguientes:

Para saber si son Polinomios de Hermite, debemos de observar si cumplen una serie de requisitos:

A) Tienen que ser ortogonales, pero no ortonormales (no cumple que sean un conjunto ortogonal y que su norma sea igual a 1). Esto, expresado en ecuación:

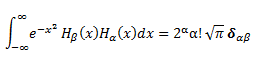
O lo que es lo mismo:

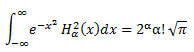
Donde la función delta de Kronecker es:

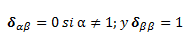
B) Poseen una función generadora (que no es mas que una serie formal de potencias, que nos da información sobre una sucesión):

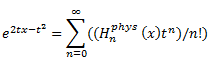
Siendo Hn el polinomio de Hermite en su forma física.

C) Formulas de recurrencia:

 

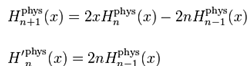
D) Descomposición en serie de funciones

Toda función continua (f) puede expresarse como una serie infinita, en términos de polinomios de Hermite (tiene lógica, ya que si no es a trozos, se presupone que será continua en R):

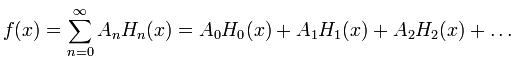
Siendo las constantes An, que se pueden calcular gracias a ésta fórmula:

 

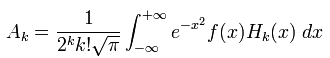
Una vez soltado el rollo de rigor, vamos a poner un ejemplo práctico para resolver estos polinomios:

>>F(x)= x^2<<

Primero vamos a descomponer esa función F(x) para luego poder desarrollarla:

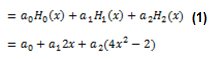
Hasta aquí solamente hemos aplicado lo que hemos visto en el apartado «d» de descomposición de funciones, y lo hemos ido sustituyendo por los polinomios contenidos en la tabla de arriba (gracias a la fórmula de Rodrigues). Ahora, vamos a juntar todo y a desarrollar ese paréntesis:

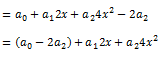
Ahora escogemos valores para a0, a1 y a2. Estos valores se los podemos dar nosotros a nuestra conveniencia:

a0=1/4

a1=0

a2=1/4

Sustituyendo en (1) nos queda: