Permutaciones circulares

En matemáticas, dado un conjunto finito con todos sus distintos elementos, denominaremos permutación a cada una de las posibles disposiciones de estos elementos de dicho conjunto. La noción de permutación puede presentarse tanto en el contexto de combinatoria como en la teoría de grupos.

Una permutación es un arreglo de todos o parte de un conjunto de objetos tomando en cuenta el orden de su ubicación. Cuando en el arreglo solo se incorporan parte de los elementos del conjunto se denomina variación. Es importante destacar que el orden es una característica significativa en la permutación, cuando variamos la disposición de los elementos decimos que permutamos dichos elementos.

Si hablamos de permutación circular estamos haciendo referencia a un caso particular de la permutación ordinaria. Las permutaciones circulares se aplican a conjuntos que se ordenan de forma circular, ya que no tienen ni principio ni final, o sea que no hay primer ni último término, por encontrarse todos los elementos en una línea cerrada.

Utilizaremos este tipo de permutaciones cuando los elementos se han de ordenar “circularmente”, por ejemplo, los presentes comensales en una mesa. Este tipo de permutaciones también son muy útiles en la resolución de problemas de la vida cotidiana, como la organización de eventos, la planificación de rutas de transporte, o la disposición de objetos en un espacio circular.

Para hallar el número de permutaciones circulares que se pueden formar con «n» objetos diferentes de un conjunto, es necesario considerar fija la posición de un elemento. Los n – 1 restantes podrán cambiar de lugar de (n – 1)! maneras distintas tomando así todas las posiciones sobre la circunferencia relativa al primer punto. Veamos la fórmula que se utiliza para calcular permutaciones circulares:

Es importante entender que esta fórmula se deriva del hecho de que estamos considerando una disposición circular, y no lineal. En una disposición lineal, tendríamos n! permutaciones posibles, ya que cada elemento podría ocupar cualquier posición. Sin embargo, en una disposición circular, una vez que fijamos la posición de un elemento, las posiciones relativas del resto de los elementos se determinan en relación a este, por lo que solo tenemos (n-1)! permutaciones posibles.

Ejemplos:

Si Calculamos las permutaciones circulares de 7 elementos tendremos lo siguiente:

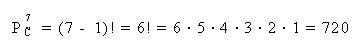
¿De cuántos modos diferentes puede sentarse al rededor de una mesa circular una madre y sus 5 hijos?

¿De cuántos modos distintos podemos ubicar las cifras del 1 al 7 en la figura siguiente?

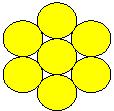
Podemos solucionar este problema como la conjunción de dos sucesos: En primer lugar ubicamos una cifra en el centro (7 posibilidades) y en segundo lugar las otras 6 cifras, las cuales por ordenarse en una circunferencia podrán permutarse de (6 –1)! maneras, por lo cual:

# maneras = 7 x 5! = 7 x 120 = 840

Las permutaciones circulares son un concepto fundamental en matemáticas y ciencias de la computación, y son utilizadas en una variedad de aplicaciones, desde la criptografía hasta la teoría de juegos. Su estudio nos permite entender mejor la estructura y las propiedades de los conjuntos finitos, y nos proporciona herramientas poderosas para resolver problemas complejos de conteo y organización.