Expresiones Algebraicas

Las expresiones algebraicas son el resultado de combinaciones de términos algebraicos, es decir, números y letras (incógnitas ó variables) unidos relacionados entre si mediante operaciones de suma, resta, multiplicación y división, cada una de ellas con sus propiedades y características.

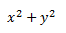
1. Constantes: Son cantidades fijas, que se expresan con letras, y que suelen «ir solas», esto es, son los conocidos términos independientes.

2. Variables: Son las famosas equis e íes, pueden cambiar de valor, por lo que las llamamos incógnitas, al no tener un valor fijo.

3. Coeficientes : Es lo que acompaña a las variables, y tienen un valor fijo, se diferencian de las constantes en que son acompaña.

Una expresión algebraica puede tomar un valor determinado, esto se consigue gracias a la sustitución en esta por un valor numérico dado, correspondiente a las variables existentes.

Si sustituimos x e y en el ejemplo anterior por 3 y 5 respectivamente:

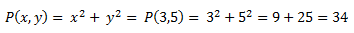
Como observáis hemos sustituido las variables por un valor concreto para conseguir un valor numérico.

**PISTA**: El orden para efectuar las operaciones correctamente es el siguiente: primero los paréntesis, potencias y raíces cuadradas, después los productos y las divisiones y por último las sumas y restas de izquierda a derecha.

Además de las operaciones básicas, también podemos encontrar en las expresiones algebraicas operaciones más complejas como las potencias y las raíces. Las potencias son una forma de expresar una multiplicación repetida, mientras que las raíces son la operación inversa a las potencias. Ambas operaciones tienen reglas y propiedades específicas que deben ser consideradas al trabajar con expresiones algebraicas.

Por ejemplo, en el caso de las potencias, cuando se multiplican dos potencias con la misma base, se suman los exponentes. Por otro lado, cuando se divide una potencia por otra con la misma base, se restan los exponentes. En cuanto a las raíces, la raíz cuadrada de un número es aquel número que, elevado al cuadrado, da el número original. La raíz cúbica es similar, pero en este caso el número se eleva al cubo.

Según sea la composición anteriormente citada, podemos distinguir varios tipos de expresiones algebraicas:

a) Monomios: Son expresiones algebraicas formadas por un coeficiente y una o varias variables siempre en producto unas con otras. Se llama «mono» porque solo posee un término algebraico:

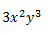
b) Binomios: Son expresiones algebraicas que poseen dos sumandos o términos algebraicos, relacionados entre sí por una operación. Son un tipo particular de polinomios. Ejemplo:

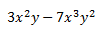
c) Trinomios: Igual que los anteriores, es un polinomio que consta de tres monomios, de forma general:

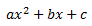
Este trinomio es el más conocido por ser una ecuación de segundo grado, sobre las cuales volveremos en otra lección.

d) Polinomios: Son un conjunto de monomios, relacionados entre sí, como los anteriores, pero estos poseen un número finito de términos, en nuestro caso, «n»:

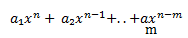
Es importante mencionar que los polinomios pueden ser clasificados según su grado. El grado de un polinomio es el mayor de los grados de sus monomios. Por ejemplo, un polinomio de grado 1 es una ecuación lineal, un polinomio de grado 2 es una ecuación cuadrática, y así sucesivamente.

Otra interesante aplicación de las expresiones algebraicas se observa en la interpretación de enunciados, por ejemplo, pensemos en un problema tal que así:

—Si la edad de Pepees xy María tiene el doble de la edad de Pepe mas cinco años, ¿Cómo se expresará la edad de María?

Se puede expresar la edad de Maríacomo 2x+5

Y si Juan tiene el doble de la edad de María, ¿Cómo se puede expresar la edad de Juan?

Pues muy fácil: como 2(2x+5).

Como observáis, estamos sustituyendo el término «edad» por una expresión algebraica, que nos ayuda a resolver el problema.

Las expresiones algebraicas también son fundamentales en la resolución de ecuaciones. Una ecuación es una igualdad que contiene una o más incógnitas. Resolver una ecuación implica encontrar los valores de las incógnitas que hacen que la igualdad sea verdadera. En este proceso, las expresiones algebraicas son herramientas esenciales.

Por último, es importante mencionar que las expresiones algebraicas son una parte fundamental de muchas áreas de la matemática y de otras ciencias. Por ejemplo, en física y en ingeniería, las expresiones algebraicas se utilizan para describir leyes y principios fundamentales. En economía y en ciencias sociales, se utilizan para modelar comportamientos y relaciones entre variables.

Hasta aquí por hoy, nos leemos en la siguiente lección.