Función secante
Está representada como y=sec(x), y es también la inversa del coseno:
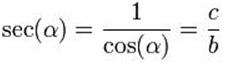
En un triángulo rectángulo, es la longitud de la hipotenusa dividida para la longitud del lado adyacente.

Las funciones trigonométricas circulares son aquellas que están referenciadas en la circunferencia. Usamos entonces la llamada circunferencia trigonométrica de radio unidad que se usa en el estudio de las funciones. De acuerdo con el cuadrante en el cual se encuentre el lado terminal de ángulo y tomando en cuenta que la distancia correspondiente a un punto cualquiera al origen de coordenadas es siempre positivo, las funciones trigonométricas pueden ser positivas o negativas. En el recuadro que se muestra a continuación podemos ver que signo corresponde a cada cuadrante si hablamos de secante.
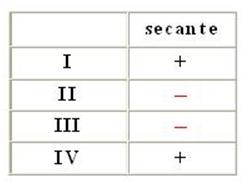
Observemos ahora la función secante y su definición como función circular:
para lo cual recurrimos al siguiente gráfico.
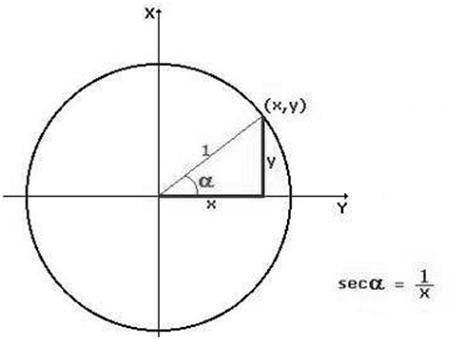
La «secante circular del ángulo a», o, simplemente, «secante de a»
La función no tiene ceros ya que para que de existir tendría que poder anularse el numerador de la fracción 1/cos x y eso no ocurre nunca porque es una constante:
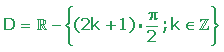
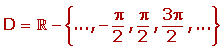
Por último me gustaría mostraros la representación gráfica:
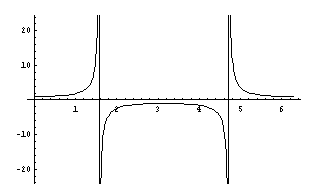
Como veis es impar ya que elementos opuestos tienen imágenes opuestas.
Se puede considerar que es creciente o decreciente pues la definición de ambas es cierta por la condición de igualdad de las dos.
