Método de bisección

Este método , que se utiliza para resolver ecuaciones de una variable, está basado en el «Teorema de los Valores Intermedios» (TVM), en el cual se establece que toda función continua f, en un intervalo cerrado [a,b], toma todos los valores que se hallan entre f(a) y f(b), de tal forma que la ecuación f(x)=0 tiene una sola raíz que verifica f(a).f(b)<0.

 

Dicho en cristiano, que si dicha función viaja del punto a al punto b, ha de pasar por m, que es cuando la función se hace cero. Ése es el punto que buscamos.

 

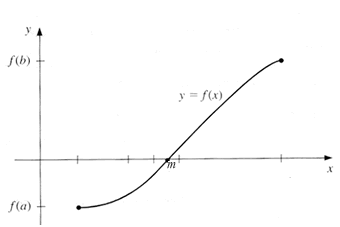
*Nota: Como veis f(a) es negativo, por tanto el producto dará negativo, eso nos asegura que existe al menos un valor de la función que es cero.

 

Una vez entendido lo anterior, veamos en detalle en qué consiste el método de la bisección:

En pocas palabras, consiste en ir dividiendo la función que hemos visto arriba en subintervalos, y hallar los puntos medios de cada uno de ellos (m), quedándonos una cosa así:

 

 

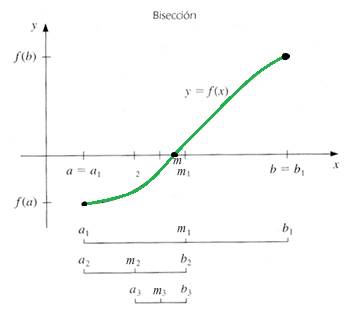
Pero veámoslo por pasos cual receta de cocina:

 

1) Elegimos dos valores iniciales a1 y b1, de tal forma que la función cambie de signo:

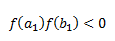
2) Realizamos la primera aproximación a la raíz, mediante la fórmula del punto medio:

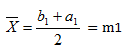
**Nota, usamos los puntos, no las funciones!! Es decir, lo que está dentro del paréntesis, NO pongáis aquí el resultado de sustituir en la función.

3) Ahora determinamos en que subintervalo se encuentra la raíz:

Si f(a1)f(m1) <0, entonces la raíz está en el subintervalo [a1,m1] y b1=m1

si f(a1)f(m1)>0, entonces la raíz está en el subintervalo [b1, m1] y a1=m1

Si f(a1)f(m1)=0, entonces aquí se encuentra la raíz

Resumido, hasta aquí, es ir hallando mitades sucesivamente hasta llegar al intervalo que nos de igual a cero.

4) Calculamos una nueva aproximación a la raíz.

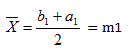
5) Evaluamos el valor relativo aproximado:

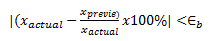
Entonces, si:

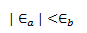
Si no cumple la condición, simplemente volvemos al paso 3.

 

>>Ejemplo:

Aproximar la raíz:

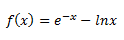
Hallar en que intervalo está la raíz con un error más pequeño que media decima

 

Lo que nos piden es que hallemos una solución para esa ecuación, y que el error que podamos tener de cálculo sea menor a 0.5. Procedemos paso a paso:

 

1) Comprobamos si es continua y vemos si cambia de signo para dos valores x1 y x2:

f es continua en el intervalo (0,+∞). Ahora debemos buscar dos valores tales que:

f(x1).f(x2)<0

x1=1-> f(x1)= 0,3679

x2=1->f(x2)= -0,5578

*Nota: Los valores elegidos son aleatorios, podéis usar otros distintos de 1 y 2, siempre que f(x) cambie de signo.

 

2) x3=(x1+x2)/2=1,5 –>∈<0,5, ya que |1-1,5|=0,5 y |2-1,5|=0,5

 

3) Momento de empezar a escoger subintervalos, escogemos el x1=1 que ya teníamos y el x3=1,5:

 

a) f(x3)= -0,1823

f(x1)= 0,3679

 

 

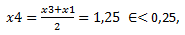
ya que |1,5-1,25|=0,25 y |1-1,25|=0,25

Como vemos el error es cada vez más pequeño, pero podemos hacerlo todavía mejor, pues todavía no está cercano a cero. Seguimos haciendo subintervalos.

b) f(x4)=0.0634

x4=1,25 ; f(x4)=0,0634

x3=1,5; f(x3)= -0,1823

 

 

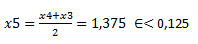
c) f(x5)= -0,0656

x4=1,25; f(x4)= 0,0634

x5=1,375; f(x5)= -0.0656

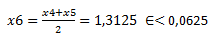
d) f(x6)= -0,0028

x4=1,25; f(x4)= 0,0634

x6=1,3125; f(x6)= -0.028

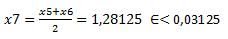
f(x7)=0,0299

Finalmente obtenemos que 1,28125 ± 0,03125 es una raíz de f(x).

** Resumen**

Como veis ha sido muy simple, tomamos dos valores de referencia, x1 y x2, hemos ido hallando la media de esos dos puntos y tomando un nuevo intervalo desde esa media, lo que conseguimos haciendo esto es «encoger» el intervalo donde se esconde la solución, haciéndolo cada vez más pequeño, y por tanto, más preciso para hallar nuestra raíz.