Crecimiento exponencial

El crecimiento exponencial o geométrico transcurre si el índice de crecimiento propio de una función es correspondiente al presente valor de dicha función, por esta razón se llama formmalmente, ley exponencial. El relacionamiento entre el tamaño de la variable dependiente con el tamaño del índice de crecimiento es establecido por razón de la ley de proporción directa. Teniendo en cuenta lo anterior, se puede sacar la conclusión de que si una magnitud M posee la variación en el tiempo de forma proporcional a su valor, estará implicando un crecimiento vertiginoso en el tiempo, lo cual correspondería a la siguiente ecuación:

Donde:

Mt corresponde valor de la extensión en el instante t > 0;

M0 corresponde al valor del inicio de la variable, valor en t = 0, si procedemos a tomar mediciones;

r corresponde a lo que sería la tasa de crecimiento instantánea, tasa media de crecimiento que ocurre en el transcurso entre t = 0 y t > 0

e = 2,718281828459…

Se hace referencia entonces al crecimiento de una función exponencial (La función exponencial, es lo que conocemos por función real e elevado a la potencia de x, e es correspodiente al número de Euler) de modo que,

Es posible desarrollar el crecimiento exponencial si se toma en la última ecuación a = 2 y x un entero. Si por ejemplo x = 4, entonces y = 2x2x2x2 = 16. Si x = 10 e y = 1.024, esto sigue continuamente.

El crecimiento exponencial tiene lugar en varias ramas científicas y tecnológicas. Buenos ejemplos de esto son, el modelo de crecimiento de las bacterias, el crecimiento demográfico, etc. Estos son acontecimientos ajustables a ecuaciones diferenciales cuyas soluciones conllevan a lo que es una función exponencial. Nombraremos ahora algunos otros ejemplos,

1. La cantidad de células que hay en un feto durante el desarrollo dentro del útero.

2. La cantidad de determinados animales en algunos entornos naturales cuando hay carencia de depredadores.

Ecuaciones diferenciales

Como ya hemos visto, el crecimiento es exponencial si ocurre que el crecimiento de la función en un punto determinado es correspondiente al valor de la función en dicho punto. Podemos expresar lo anterior por medio de una ecuación diferencial de primer orden. Este tipo de ecuación diferencial es una ecuación diferencial ordinaria dónde se encuentran derivadas de primer orden en proporción a una variable independiente, veamos:

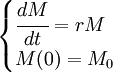
M0 corresponde al valor de inicio de la magnitud, de la cual se estudia el crecimiento exponencial ( t = 0). Cualquiera sea el instante de tiempo ulterior en esta ecuación tendremos como resultado que:

Para t > 0 podemos ver que,

siempre y cuando el crecimiento sea de forma positiva r > 0

El patrón de crecimiento de Malthus, (a veces se denomina exponencial simple) es basicamente un modelo o patrón del crecimiento exponencial que corresponde a un índice constante de interés compuesto. El modelo de Malthus se denomina en general «El modelo de Malthusiano» en honor el demógrafo y economista político británico, Thomas Robert Malthus . En su importante ensayo llamado «Ensayo sobre los principios de la población» afirmó que el crecimiento de la población algún día llegaría a sobrepasar la oferta alimenticia en el año 1798, lo cual tuvo gran influencia en la política. Afortunadamente la predicción de Malthus no se cumplió, ya que el avance de las industrias elevaron la elaboración de productos alimenticios en naciones con buena economía y también se fue reduciendo en estas naciones la tasa de fertilidad.