Exponenciación

Podemos decir que la exponenciación es una operación que se define en lo que es un álgebra sobre un cuerpo normada completa o álgebra de Banach. Lo importante de esto es que se generaliza la función exponencial de los números reales.

Cuando por ejemplo a y b corresponden a dos números enteros la operación puede definirse en términos algebraicos elementales. Pero ciertos números de problemas físicos llevaron a tratar de generalizar la fórmula anterior a valores de b no siendo enteros. Cuando b = 1/2 la operación es equivalente a lo que llamamos una raíz cuadrada. De modo que la exponenciación trata de generalizar una operación como:

Habitualmente dicha operación puede ser reducida al cálculo de la siguiente operación:

Se generaliza entonces este tipo de operación a casos donde el exponente no es precisamente un número real.

Para que sea mas sencillo entender lo que es una exponenciación y saber a que nos referimos cuando hablamos de exponente, prestemos mucha atención a lo siguiente. Tomemos como ejemplo una expresión matemática que tenga incluidos dos términos, los cuales se denominan base a y exponente n. Un exponente se utiliza para indicar la multiplicación repetida, elevando una base a n. El proceso de elevar una base a un exponente se llama potenciación. Entonces si a es un número real y n un número real se definirá como:

Entonces:

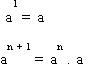
Esto varía según el conjunto numérico al cual pertenezca dicho exponente.

Si a es un número real no nulo, se define entonces como:

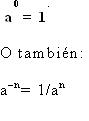
De lo anterior podemos deducir cuales serían las reglas que habitualmente se utilizan en la exponenciación, veamos cuales serían:

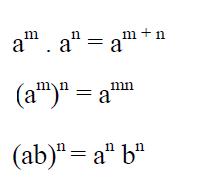
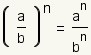
En la regla anterior podemos ver que la exponenciación distribuye a través de la división.

En este último caso observamos que el numerador de un exponente fraccionario es un exponente, mientras que el denominador es una raíz.