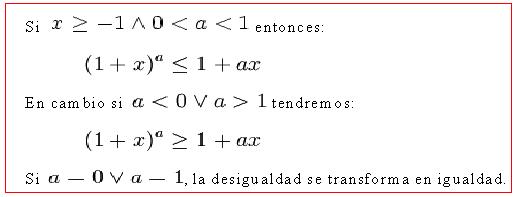
Desigualdad de Bernoulli
Una desigualdad es una relación que existe entre dos cantidades en las cuales hay un diferente valor. O sea que sería lo contrario a lo que ocurre en una igualdad. En la desigualdad, los términos se relacionan por un símbolo de «mayor que» (>) o «menor que» (<). También existen algunos términos que derivan de los dos anteriores. Si alguno de estos dos símbolos está acompañado por una línea horizontal por debajo, significa "mayor o igual que" o "menor o igual que". Un ejemplo de una desigualdad podría ser:
Algunos problemas matemáticos se plantean como desigualdades en lugar de plantearse como ecuaciones. Dichas desigualdades se resuelven de manera semejante a una ecuación. Algunas de ellas se usan con tanta frecuencia que se les ha puesto nombre, como por ejemplo la Desigualdad de Bernoulli. Se denomina de esta forma en honor a la familia Bernoulli ya que fue utilizada por primera vez por los miembros de dicha familia, de la cual eran parte importantes matemáticos y físicos suizos procedentes de la ciudad de Basilea. Irrumpieron en el mundo científico a finales del siglo XVII.
La desigualdad de Bernoulli es una desigualdad que se aproxima a la exponenciación de 1 + x. Indica que para cada número entero r ≥ 0 y cada número verdadero x > −1 si el exponente r es uniforme, entonces la desigualdad es válida para todos los números reales x. Podemos decir entonces que para cada número entero r ≥ 2 y cada número verdadero x ≥ −1 con x ≠ 0.
Esta desigualdad se utiliza frecuentemente como el paso crucial en prueba de otras desigualdades y es utilizada en la resolución de problemas. Veamos otra forma de explicarla: