Espiral logarítmica
La espiral logarítmica en matemática esta incluida en la categoría de las curvas mecánicas que son aquellas cuyas ecuaciones no son polinomios. La espiral logarítmica debe el nombre a la ecuación de la siguiente forma:
![]()
C y K son constantes , e=2,71828182 base neperiana de losl ogaritmos naturales o neperianos, r es el radio de posición del punto y luego tenemos el ángulo girado. Si despejamos de la ecuación dicha el ángulo en función del radio, obtenemos la siguiente ecuación en donde el ángulo es equitativo al logaritmo del radio.
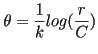
La espiral logarítmica aparece en un escrito de descartes por primera vez en el año 1638, pero fue denominada luego como la conocemos por Jackob Bernoulli, en uno de sus trabajos donde maravillado por la belleza de esta figura la denomina “Spira Mirabilis”. Otra forma de denominarla es espiral equiangular. Este tipo de espiral es muy interesante desde el punto de vista geométrico. Es también la curva definida por un objeto que se mueve con velocidad lineal constante y velocidad angular. Se le suele llamar también espiral de crecimiento puesto que en la naturaleza hay cosas que se desarrollan a velocidades constantes en simultaneidad hacia afuera y alrededor de un objeto. Este espiral es el que mas podemos observar en la naturaleza, en el reino vegetal, en las formas de las galaxias, en las conchas de algunas especies de moluscos, etc. Etc. Es también usado en el arte desde épocas prehistóricas.
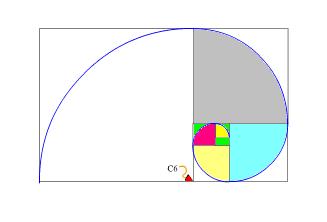
Para construir una espiral logarítmica podemos proceder de la siguiente forma. Si construimos sucesivamente rectángulos áureos, (o sea rectángulos cuyos lados son proporcionalmente igual a la razón aurea, por ejemplo las hojas de papel de tamaño carta de 11 x 8 pulgadas aproximadamente tienen una proporción similar a la aurea de 1.37) es decir trazamos cuadrados dentro de un rectángulo original unas cinco veces obtendremos cinco cuadrados dentro de dicho rectángulo. Si tenemos esto lo que debemos hacer es apoyar un compás en el punto c1, tal cual se muestra en la figura y luego trazar un cuarto de círculo en el cuadrado, de esto forma repetimos este paso en los puntos c2, c3, c4 y c5, obteniendo así la espiral logarítmica.
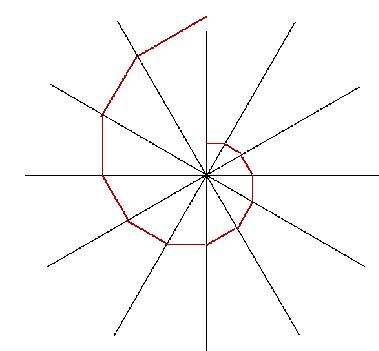
También podemos trazar la espiral a través de un transcurso de aproximaciones sucesivas. En este caso comenzamos con una agrupación de rayos separados por un ángulo constante, luego elegimos un punto sobre uno de los rayos que sea lo suficientemente cercano al centro y allí trazamos una línea perpendicular al rayo que pase por el punto que hemos elegido ,tal como se muestra en la siguiente figura:
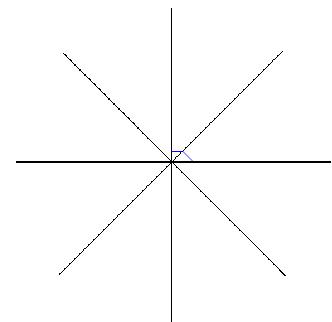
De esta forma tendremos determinado un punto sobre el rayo continuo en el sentido horario. Entonces nuevamente trazamos la perpendicular al rayo adyacente por el punto que acabamos de hallar y encontrando un tercer punto sobre el siguiente rayo en este caso. Continuando con este proceso tendremos como resultado una figura semejante a la espiral. Véase el ejemplo a continuación.