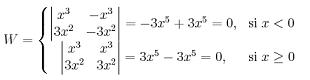El Wronskiano
Los Wronskianos son funciones denominadas de tal forma en honor al físico, filósofo y matemático polaco Josef Hoene-Wronski (1778-1853). Son fundamentales en el estudio de los sistemas ecuaciones diferenciales. Dichos sistemas surgen en problemas que se relacionan principalmente con las variables dependientes las cuales son función de la propia variable independiente. Son de utilidad para determinar si dos funciones son independientes linealmente y de esta forma crear un conjunto solución que a la vez respete la teoría de las ecuaciones diferenciales, veamos entonces un ejemplo.
a, b y c son constantes en la siguiente ecuación diferencial, que a la vez es de segundo orden, de primer grado y homogénea.
![]()
Es posible que la solución a esta ecuación sea una combinación lineal como la que vemos a continuación,
![]()
Debemos comprobar lo anterior y una de las formas para hacerlo es anotar la ecuación en forma de operador. Siendo así nos quedaría:
![]()
Las raíces de esto son λ1 y λ2
Como el polinomio es de segundo grado podemos obtener dos raíces, las cuales pueden ser, reales diferentes, reales iguales o complejas conjugadas.
Para probar si es posible realizar esta combinación es posible el uso del Wronskiano como determinante. Los resultados a comprobar son:
![]()
Es de gran importancia tener en cuenta que la solución general es,
![]()
Es una combinación lineal que corresponde a las dos soluciones. Se conoce que las raíces son reales y diferentes, por lo cual si se utiliza la fórmula general, el discriminante de esta será mayor que las raíces las cuales son reales y diferentes en este caso:
![]()
En la primera línea se deben colocar las soluciones que se probarán si son dos, el wronskiano es entonces de 2×2. En la línea secundaria se ubicarán las derivadas de las soluciones. Entonces si dan como resultado,
![]()
Las derivadas serán estas,
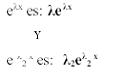
Cuando son colocadas en el determinante tenemos lo siguiente,
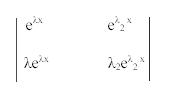
Se resuelve esto con la operación que sigue,
![]()
El Wronskiano es entonces:
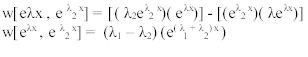
Si el Wronskiano es diferente de cero, las funciones son linealmente independientes. Si las raíces son diferentes, entonces no vale cero. Por lo tanto la solución de este ejercicio no puede ser cero puesto que las raíces son diferentes y el único punto donde la exponencial tiene valor cero es si x corresponde a menos infinito. Como el wronskiano es diferente de cero se comprueba que las soluciones son linealmente independientes.
![]()
En otro caso si el discriminante es igual a cero las raíces serán reales e iguales. Si se realiza el Wronskiano con dos raíces iguales, nos da como resultado cero, por lo cual tendríamos soluciones linealmente independientes.
En caso que el discriminante sea menor que cero las raíces serán lo que llamamos complejas conjugadas.
Es importante saber que las funciones son linealmente independientes a excepción de que el exponencial sea cero, o sea si x, tiende a menos infinito. Si se consideran funciones de tercer grado puede que esto no sea de tal forma ya que por ejemplo el valor absoluto de x elevado al cubo puede ser escrito de la siguiente forma:
![]()
Se puede verificar que esta función es linealmente independiente aunque su Wronskiano sea cero.