Congruencias

¿Qué son las congruencias? ¿Qué significan? ¿Para qué se utilizan….?

Nos enfrentamos en este nuevo post a un concepto nuevo, las congruencias, un concepto que se utiliza en Álgebra y más concretamente en la parte de Teoría de conjuntos.

Además, este nuevo concepto, ha significado desde tiempos muy remotos la evolución y desarrollo de diversas aplicaciones, un ejemplo muy importante de ello es la criptografía.

DEFINICIÓN:

Diremos que dos números a y b son congruentes módulo n, y escribimos a≡b (n), si y sólo si, a es igual a b más la suma de un múltiplo de n: a=b+kn. Que también podríamos expresarlos como: a-b≡(n), es decir, que a-b es un múltiplo de n.

Ejemplos:

Para comprender un poco este nuevo concepto veamos algunos ejemplos sencillos:

a) El 8 es congruente con 5 módulo 3, ya que: 8≡5(3)→8=5+1•3

Como hemos dicho en la definición a y b son números enteros, por tanto pueden ser números negativos, por ejemplo:

b) El 13 es congruente con -2 módulo 3, ya que: 13≡-2(3)→13=-2+5•3

PROPIEDADES:

Utilizando las propiedades de los números enteros podemos demostrar las siguientes propiedades:

1. Un número es congruente consigo mismo módulo n: a≡a (n)

2. Si a es congruente con b módulo n, entonces también se cumple el recíproco: a≡b (n) entonces también se cumple que b≡a (n)

3. Si a es congruente con b módulo n, y a su vez b es congruente con c módulo n, entonces a es congruente con c módulo n: a≡b (n) y b≡c (n), entonces a≡c (n)

4. Sean a≡a´ (n) y b≡b´ (n), entonces se cumple que:

a) a+b≡a´+b´ (n)

b) a•b≡a•´b´ (n)

Para cualquier número c perteneciente a los números enteros se cumple que:

c) a+c≡a´+c (n)

d) a•c≡a´•c (n)

e) Si a≡a´ (cn)→a≡a´(n), siempre y cuando c sea distinto de cero.

APLICACIONES:

Ya se que a veces puedo resultar muy pesada… pero como todo en matemáticas (aunque a veces no nos lo parezca), las congruencias tienen varias aplicaciones:

– Podemos resolver ecuaciones con números grandes reduciéndolos a números más pequeños.

– Si es posible resolver ecuaciones, podemos ampliar este proceso como es evidente a la resolución de sistemas de ecuaciones.

– Y una de las aplicaciones más importantes es establecer los criterios de divisibilidad.

CRITERIOS DE DIVISIBILIDAD

Antes de establecer los criterios de divisibilidad es necesario definir un concepto nuevo:

Llamamos restos potenciales de p módulo n, a los restos que se obtienen de dividir las sucesivas potencias de p módulo n, y que por tanto podemos expresar de la siguiente manera:

Donde los ri son los restos obtenidos.

A partir de esta definición se pueden deducir varias cosas:

1) Que el primer resto siempre es 1.

2) Que los valores de estos restos son finitos ya que tienen que ser menor que n, por tanto llegará el caso que comiencen a repetirse.

3) Que la condición anterior, nos permitirá crear un método recurrente.

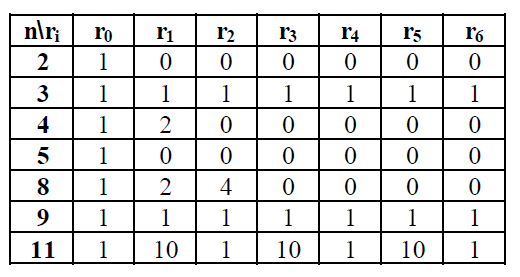
Utilizando la siguiente tabla en la que aparecen los restos potenciales de 10 en los módulos 2,3,4,5,8,9 y 11, vamos a dar algunos de los criterios de divisibilidad más importantes:

a) Criterio de divisibilidad del 2: Un número es divisible por 2 siempre y cuando la última cifra sea divisible por 2, es decir, siempre y cuando el número sea par.

b) Criterio de divisibilidad del 3: Un número es divisible por 3 siempre y cuando la suma de sus cifras sea un múltiplo de 3.

c) Criterio de divisibilidad del 5: Un número es divisible por 5 siempre y cuando termine en 0 o en 5.

d) Criterio de divisibilidad del 11: Un número es múltiplo de 11 siempre y cuando a la suma de las cifras que ocupan lugar impar le restamos las que ocupan lugar par el resultado que se obtiene es un múltiplo de 11.

Ejemplo: Estudiar si el número 30876 es múltiplo de 2, 3, 5 y 11.

a) Es múltiplo de dos porque es un número par.

b) Es múltiplo de 3 porque la suma de sus cifras es un múltiplo de 3: 3+0+8+7+6=24=8•3.

c) No es múltiplo de 5, porque no termina en 0 o 5.

d) No es múltiplo de 11, porque: suma cifras impares-suma cifras impares = (3+8+6)-(0+7)=10 que no es múltiplo de 11.