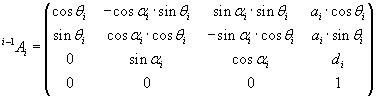Cinemática directa
Se denomina cinemática directa a una técnica que es utilizada en gráficos 3D por computadora, para solucionar y calcular la posición de partes de una estructura articulada a partir de sus elementos fijos y las transformaciones que se provocan por las articulaciones de la estructura.
Un ejemplo típico sobre el cual realizar este tipo cálculos es un robot que se puede considerar como una cadena cinemática, formado por cuerpos rígidos o eslabones enlazados por articulaciones. Se puede instituir un sistema de referencia fijo situado en la base del robot, y describir la localización de cada uno de los eslabones con respecto a dicho sistema de referencia. Una pieza rígida A depende jerárquicamente de otra B si, para lograr la parte fija de la estructura que sería la base del robot desde A, se debe pasar por B. Para calcular la posición de una pieza rígida de la estructura se deben calcular las posiciones de todas las piezas de las que depende. De esta forma, el problema cinemática directo se reduce a hallar una matriz homogénea de transformación T que relacione la posición y orientación del extremo del robot respecto del sistema de referencia fijo ubicado en la base del mismo. Esta matriz T será función de las coordenadas articulares. Bibliotecas gráficas de uso generalizado, como OpenGL, están diseñadas para facilitar estos procesamientos de datos y llevarlos a cabo eficazmente mediante pilas de matrices.
En la resolución de la cinemática directa de un robot, el primer paso que se debe realizar es construir los sistemas de referencia D-H a partir de una situación inicial del robot. Un problema cinemático directo consistirá en determinar cuales son la posición y orientación del extremo final del robot, en relación a un sistema de coordenadas que se toma como referencia, si conocemos previamente los valores de las articulaciones y los parámetros geométricos de los elementos del robot.
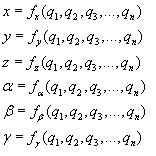
Generalmente un robot de n grados de libertad se compone por n eslabones unidos por n articulaciones. A cada eslabón se le puede atribuir un sistema de referencia utilizando las transformaciones e innovaciones homogéneas, es posible entonces representar las rotaciones y traslaciones relativas entre los distintos eslabones que forman al robot. La matriz de transformación homogénea que representa la posición y orientación relativa entre los diferentes sistemas asociados a dos eslabones consecutivos del robot se designan i−1Ai. La matriz 0Ak, resultante del producto de las matrices i−1Ai con i desde 1 hasta k, es la que representa la cadena cinemática que forma el robot. Cuando se consideran todos los grados de libertad, a la matriz 0An se le llama T. Así, dado un robot de 6gdl, se tiene que la posición y orientación del eslabón final será una consecuencia por la matriz T:
![]()
Para representar la relación que existe entre dos sistemas de referencia asociados a eslabones, se utiliza la representación Denavit – Hartenberg (D-H) Este método matricial permite establecer de manera metódica un sistema de coordenadas ligado a cada eslabón i de una cadena articulada. También permite pasar de un sistema de coordenadas a otro mediante 4 transformaciones básicas que dependen de las características geométricas del eslabón. Estas transformaciones consisten en una sucesión de rotaciones y traslaciones que permiten relacionar el sistema de referencia del elemento i con el sistema del elemento i − 1.
. Dichas transformaciones serían:
La rotación alrededor del eje zi−1 un ángulo Өi.
La traslación a lo largo de zi−1 una distancia di.
La traslación a lo largo de xi una distancia ai.
La rotación alrededor del eje xi un ángulo αi.
Teniendo estos valores que serían los parámetros D-H del eslabón i, la matriz de transformación que relaciona los sistemas de referencia {Si−1} y {Si} sería la siguiente:
![]()
Desarrollando esta expresión nos quedaría: