Método Ruffini

 

¿Cuántas veces nos hemos encontrado con un polinomio en el cual nos es imposible conocer las raíces para descomponerlo en binomios más sencillos de la forma (x-r) ?

 

Bien, no entremos en pánico, porque hace ya bastantes años (en 1814 más concretamente), un señor llamado Paolo Ruffini, se sacó de la manga un método muy útil para factorizar polinomios de grado n mediante divisiones, y se conoce como la «Regla de Ruffini».

 

Pero veámoslo en la práctica con un ejemplo, supongamos que tenemos un cociente de polinomios P(x) y Q (x) tal qué:

 

P(x)= (x^4 -16)

Q(x)= (x-2)

 

Como veis resulta complicado dividir ese cociente, pues necesitamos saber las raíces de P(x) primero, no hay forma matemática de hacer esa división directamente, por ello nos ayudamos de Ruffini:

 

-Primer paso

 

Lo primero que debemos de hacer es mirar el polinomio P(x) y colocar sus coeficientes (lo que está pegado a las equis) en una línea rellenando los coeficientes que no tengamos con ceros:

 

 

    1 0 0 0 -16

 

 

-Segundo paso:

 

 

Ahora, a la izquierda trazaremos una línea horizontal, y después un poco más abajo otra línea vertical, en donde se crucen, por fuera, pondremos nuestro divisor cambiado de signo, en este caso tenemos el -2, por lo que pondríamos el 2 en positivo:

 

   

 

 

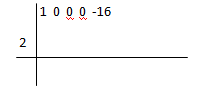
-Tercer paso:

 

Por último, operamos, para ello, debemos bajar el primer coeficiente y después multiplicarlo por el divisor de la izquierda (el dos) y sumaríamos esos dos coeficientes:

 

    

 

 

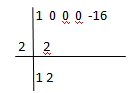
– Cuarto paso:

 

Ahora seguimos haciendo lo mismo hasta llegar al último de los coeficientes, en donde deberemos de tener el último de nuestros coeficientes a cero, que es lo que llamamos el resto.

 

 

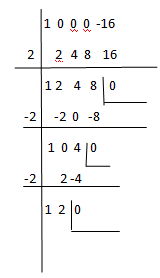
Por tanto: P(x)= (x-2)(x+2)(x+2)(x+2)

**PISTA** : Intenta fijarte siempre en el ultimo coeficiente, éste te dará que divisor debes emplear, escogiendo siempre múltiplos (si te das cuenta 16, 8 y 4 no son más que potencias de 2, pues son 2, respectivamente).

**PISTA**: Acordaos de cambiar de signo los divisores de la izquierda cuando escribáis los binomios, si os fijáis los he puesto en orden, 2, -2 y -2, esto es muy importante ya que por un signo os puede cambiar todo el polinomio.

Como veis he realizado dos veces más los mismos pasos, solo para que veáis lo sencillo que es, además, es mucho mejor simplificar lo máximo posible, pues luego para realizar los cálculos nos vendrá muy bien. En este caso, para realizar la división de P(x) entre Q(x):

 

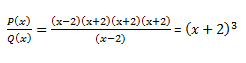
Nota: He puesto los (x-2) y (x+2) como binomio al cuadrado por simplificar cálculos.

Nota2: En este caso hemos tenido la suerte de que los cocientes nos salieron todos cero, de ser el caso, si por ejemplo al final en vez de tener cero tuviese 5, la solución quedaría así:

(x-2)(x+2)(x+2)(x+2+5), ese 5 final iría en lugar del último resto.