Fracciones decimales
Una fracción decimal es aquella en la cual el número de abajo, o sea el denominador, es una potencia de diez, como sería 10; 100; 1000; 10000, etc. Es posible entonces escribir fracciones que sean decimales con un punto decimal y sin el denominador. Esto facilita enormemente el calcular las operaciones, tales como las sumas o multiplicaciones de la fracciones. Los números decimales son en sí un tipo de número fraccionario. Por ejemplo el decimal 0.5 representa exactamente la fracción 5/10. La fracción 43/100 es también la representación de un decimal, es lo mismo entonces que 0.43.

Las fracciones decimales son entonces lo que corresponde a las partes de un entero que se ha partido en una decena de partes iguales o una centena, etc., etc. Es muy importante tener en claro que lo que generalmente llamamos números decimales, o sea los números con coma decimal, están expresando una fracción decimal.
Además de las operaciones básicas, las fracciones decimales también se pueden utilizar en operaciones más complejas como la división y la multiplicación de fracciones. Por ejemplo, si queremos dividir 0.75 por 0.25, simplemente dividimos los números como si fueran enteros (75 dividido por 25) para obtener 3. Del mismo modo, si queremos multiplicar 0.4 por 0.2, simplemente multiplicamos los números como si fueran enteros (4 multiplicado por 2) para obtener 8, y luego colocamos el punto decimal en el lugar correcto para obtener 0.8.
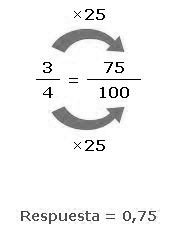
Es posible también convertir fracciones a decimales. Para esto primero debemos encontrar un número que podamos multiplicar por la parte de debajo de la fracción o sea el denominador para lograr que se convierta en una potencia de diez. Luego también multiplicamos la parte superior de la fracción o sea el numerador. Como último paso escribiremos el número de arriba, colocando la coma en el lugar apropiado, o sea un espacio desde el lado derecho por cada cero en el número inferior. Veamos algunos ejemplos de esto:
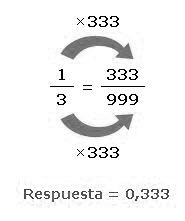
Aquí tenemos un ejemplo en el cual no hay forma de multiplicar el 3 para que se vuelva 10, 100 o cualquier potencia de 10. En este caso calculamos un decimal aproximado eligiendo un múltiplo en este caso 333: Veamos el ejemplo:
Además, es importante mencionar que las fracciones decimales también se pueden utilizar para representar números irracionales, como la raíz cuadrada de 2 o el número pi. Estos números no se pueden representar exactamente como fracciones decimales, pero se pueden aproximar a una fracción decimal con un cierto grado de precisión. Por ejemplo, la raíz cuadrada de 2 se puede aproximar a 1.41, y el número pi se puede aproximar a 3.14. Estas aproximaciones son útiles en muchas aplicaciones prácticas, como en la ingeniería y la física.
