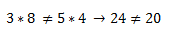Fracciones equivalentes

Las fracciones equivalentes son aquellas que tienen el mismo valor o que la representación sobre la cantidad que representan es la misma.

Pensemos en una tarta cortada en ocho trozos:

 

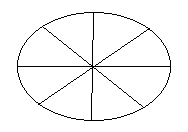
Ahora supongamos que viene alguien y se come 2 trozos, la representación en fracción de lo que nos queda sería 6/8, es decir, tenemos 6 trozos de 8 totales, quedándonos así nuestra tarta:

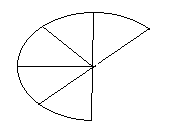
¿ Y si en lugar de partirla en 8 hubiese sido en 4 trozos? Quedaría como esto:

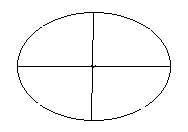
Y ahora pensemos que llega alguien y se come un trozo, a representación de lo que nos queda en fracción sería 3/4:

Pues bien, ¿Qué diríais si os dijese que ambas personas comieron una cantidad de tarta equivalente? ¿Qué no?¿ Lo decís por el dibujo? Seguramente os parecerá que el primero ha comido más, pero tened en cuenta que sus trozos (fracciones) eran más pequeños, y nuestro segundo tragón comió un trozo enorme.

Mirad bien las fracciones que tenemos y veréis que una es la mitad de la otra, si dividimos ambos términos (numerador y divisor por 2):

 

 

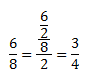
Nos queda entonces la misma fracción transformada. Podemos decir entonces que, multiplicando o dividiendo por el mismo número en numerador y denominador, obtendremos una fracción equivalente de la anterior. Eso sí, tened en cuenta que os tiene que dar exacta la división, es decir, los 6/8 no los podríamos dividir entre 3 por ejemplo, porque 8 entre 3 no nos da un número exacto. Tampoco se os ocurra restar o sumar, ya que eso modificará totalmente la fracción dando otra totalmente distinta.

Para dejarlo claro, pensad en las escalas de dibujo, en realidad son indicaciones de cómo hemos de multiplicar o dividir cada centímetro de nuestro dibujo para representarlo al mismo tamaño que el objeto real.

Vamos a ver un último ejemplo para curarnos en salud y que no quede ninguno confuso:

 

 

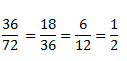
Cuando una fracción nos queda como en este caso, en la que no podemos dividir más, se dice que está simplificada.

Ahora que tenemos claro cuando son, os pongo otro ejemplo más, pero esta vez de un caso en el que las fracciones no serían equivalentes entre sí:

 

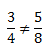
A simple vista en este caso se ve que no podemos multiplicar ni dividir de tal forma que la primera fracción sea igual que la segunda, pero si os encontráis con unas fracciones las cuales sean difíciles de saber si son equivalentes o no a simple vista, no tenéis más que multiplicar numerador por denominador en cruz y ver si os da lo mismo. En el ejemplo de arriba: