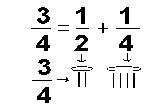Fracciones unitarias
Como ya sabemos una fracción o quebrado, es un número que se logra obtener al dividir un total es partes iguales. Se representan matemáticamente por números que están escritos uno sobre otro, al número superior lo llamamos numerador, mientras al número de la parte inferior lo llamamos denominador. El conjunto de todas las fracciones equivalentes, (o sea fracciones diferentes que representan el mismo valor) se llama número racional. Existen muchas formas de clasificar fracciones, (propias, impropias, reducibles, irreducibles, etc. Etc.) Pero aquí nos limitaremos a ver que es una fracción unitaria.
Una fracción unitaria representa a un número racional. Es una fracción que tiene como numerador la cifra 1 y como denominador tiene un número entero positivo. O sea que las fracciones unitarias tienen como numerador la unidad. Veamos algunos ejemplos:
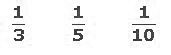
Podemos observar que este tipo de fracciones son entonces los inversos de números enteros positivos. Cuanto más grande sea el denominador menor será el número racional que representa la fracción.
Si multiplicamos fracciones unitarias tendremos como resultado otra fracción unitaria. Siempre ocurrirá esto con el producto de dos fracciones unitarias. Observemos entonces los siguientes ejemplos:
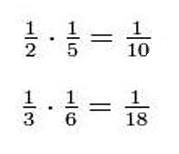
El resultado de la división de dos fracciones unitarias o sea el cociente, será otra fracción unitaria solo si el denominador es un “múltiplo del numerador”. Un caso insignificante es cuando la fracción por la cual dividimos es 1/1.
Si sumamos o restamos fracciones unitarias, es posible obtener como resultado otra fracción unitaria, pero no es lo que en general pasa, veamos algunos ejemplos con estas operaciones:
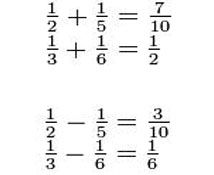
Debemos tener en claro que cualquier número racional positivo se puede escribir como la suma de fracciones unitarias, lo que dará como resultado una fracción egipcia aunque la expresión no será la única. Este tipo de fracciones eran utilizadas por Egipto en la antigüedad. Les dejaremos entonces un claro y sencillo ejemplo de lo que son las fracciones Egipcias, aunque más adelante entraremos en más detalles.