Fracciones continuas
El origen de las fracciones continuas se remonta a la antigua Grecia, es uno de los temas más antiguos dentro de las matemáticas. El primero en estudiar este tipo de fracciones fue Euclides quien vivió en el siglo 3 a.c en Alejandría. Una fracción continua trata de dar una expresión conveniente a los números reales para estudiar sus propiedades aritméticas más que la expresión en decimales. Comencemos a ver entonces este tema más de cerca. Una fracción continua es una expresión de la siguiente forma:
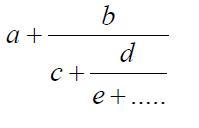
Debemos tener en cuenta que en esta expresión los números pueden representar cualquier cantidad siempre y cuando las cifras del denominador y numerador sean números enteros positivos. La representación en una fracción continua de un racional es en general corta, y es única siempre que no termine en 1. Sabemos entonces que en el siguiente ejemplo a1, a2, a3… tendremos números enteros positivos.
Cuando el número de cocientes es finito, entonces diremos que tenemos una fracción continua que es limitada ya que como bien dijimos los números son finitos, podemos decir entonces que la fracción continua es simple. En cambio si el número de cocientes es limitado tendremos lo que se llama una fracción continua infinita.
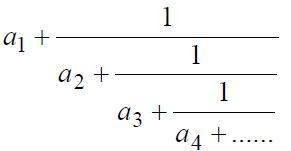
Veremos ahora una clara representación de como resolver y proceder en una fracción continua entonces supongamos que si m/n es la fracción dada, lo que debemos hacer es dividir m por n, de esta forma obtendremos un cociente a1 y el resto r1, entonces nos quedaría de la siguiente forma:
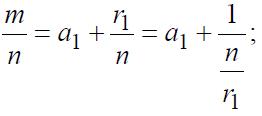
Luego de esto dividimos n por rl obteniendo así el cociente a2 y el resto r2, veamos ahora como nos queda:
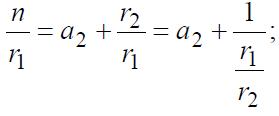
Entonces seguiremos desarrollando este proceso de la misma forma, hasta llegar a una división exacta donde terminará este proceso. De este modo toda fracción que posea un número entero positivo en su numerador y denominador puede transformarse en una fracción continua limitada. En caso de querer verificar, lo que debemos hacer es realizar las operaciones indicadas en la fracción que obtuvimos para llegar así a la fracción original.
Existen también otro tipo de fracciones que son las llamadas, fracciones continuas periódicas. Se trata de una expresión irracional cuadrática que puede expresarse como una fracción continua infinita en donde sus cocientes se repiten periódicamente. O sea que se utilizan para calcular raíces cuadradas. Los términos propios de una fracción continua se repetirán únicamente si representa un numero racional cuadrático.
