Álgebra libre
El álgebra abstracta es el campo de las matemáticas que se encarga de estudiar las estructuras algebraicas como las de grupo, anillo, cuerpo o espacio vectorial. Dichas estructuras fueron definidas debidamente en el siglo XIX. El estudio de este tipo de álgebra fue motivado por la necesidad de más puntualidad en las definiciones matemáticas. Esto ha permitido observar claramente cosas específicas en las afirmaciones lógicas en las cuales se basa la matemática en general. Los algebristas descubrieron a lo largo de la historia que algunas estructuras lógicas en apariencia diferentes muy a menudo pueden determinarse de la misma forma con un pequeño conjunto de axiomas. El término álgebra abstracta es utilizado para diferenciar este campo del álgebra elemental que es el álgebra que conocemos en escuela secundaria y que se encarga de mostrar las reglas correctas para operar con fórmulas y expresiones algebraicas que corresponden a los números reales y números complejos. El álgebra abstracta se dio a conocer durante la primera mitad del siglo XX como álgebra moderna.
Una de las ramas que estudia el álgebra abstracta, es el álgebra libre la cual es el análogo no conmutativo del anillo de polinomios. Se dice que una operación binaria es conmutativa cuando el resultado de la operación es el mismo cualquiera que sea el orden de sus elementos.
Para entender que es el anillo de polinomios supongamos que A es un anillo y S cualquier conjunto. El conjunto A[S] de todos los objetos como por ejemplo:
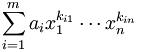
En el cual:
![]()
Tenemos números naturales y es desigual para los distintos valores de i, diremos entonces que es un anillo de polinomios con indeterminadas en S sobre A.
Un anillo es entonces una estructura algebraica que se forma por un conjunto y dos operaciones que se relacionan mediante la propiedad distributiva. Se dice que un anillo A es conmutativo si A =Z(A). El ejemplo más simple de anillo conmutativo es el conjunto de los números enteros, junto con las operaciones de suma y multiplicación de enteros.
Tomemos ahora otro ejemplo, siendo R un anillo. El álgebra libre en n indeterminada, X1…, Xn, es el anillo que se genera por todas las diferentes combinaciones lineales de los productos de las variables. Este anillo se expresa como R
A diferencia de un anillo polinómico, las variables no conmutan. Por ejemplo X1X2 no es lo mismo que X2X1. Sobre un cuerpo, el álgebra libre en n indeterminada se puede formar como el álgebra tensorial de un espacio vectorial n-dimensional. (Para un anillo de coeficientes, la misma formación es válida si tomamos el módulo libre en n generadores.)
