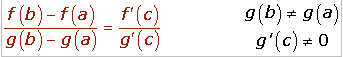Agustin Louis Cauchy

Un día más vamos a estudiar a otro de los grandes matemáticos de la historia: Agustín Louis Cauchy. Un matemático francés conocido sobre todo por sus trabajos en la teoría de grupos. Además también estudió la convergencia y divergencia de series infinitas, así como otros conceptos del análisis matemático como son las derivadas, las ecuaciones diferenciales y los determinantes. Algunos de sus teoremas muy importantes serán citados a continuación en nuestro artículo de hoy.

Augustin Louis Cauchy nació en París en 1789 en una época que coincide con un período del a historia muy conocido: la revolución francesa. De su educación matemática se ocuparon otros dos grandes matemáticos amigos de su padre: Laplace y Lagrange. Después de graduarse trabajó como ingeniero en la flota de Napoleón, la cual se estaba preparando para la invasión a Inglaterra, no obstante; no dejó en ningún momento de lado las matemáticas, ya que se llevó consigo una copia de los trabajos de sus maestros Laplace y Lagrange.

Publicó su primer trabajo en 1811 en el que demostraba que los ángulos de un poliedro convexo quedan determinados por sus caras. Pero como ya hemos comentado al principio, fue simplemente eso, el principio, un año después vuelve a escribir sobre geometría, un artículo sobre polígono y poliedros. Consiguió el anhelado trabajo que tanto le costó en 1815 como profesor ayudante de análisis en la École Polytechnique. Pero lo que realmente le llevó a conseguir la plaza en la Academia Francesa de Ciencias, fue la prueba de la afirmación de Fermant sobre números poligonales.

Las bases del análisis infinitesimal también se deben a este gran personaje. Y también es él, el que da los conceptos de función, límite y continuidad de la manera que se conoce actualmente.

Pero, como ya es común en nuestros anteriores personajes, no solo destacó en varios campos de las matemáticas, si no que también desarrolló trabajos de física matemática y la mecánica teórica, donde destaca la teoría de la elasticidad y la teoría de la luz.

Murió en el 1857 y en sus últimos semanas dijo una de las frases que mejor resumen su vida: “No me imagino una vida más plena que una vida dedicada a la matemática”.

Una vez que ya hemos conocido un poco más a nuestro amigo de hoy, vamos a ver algunos de sus más famosas aportaciones (aunque nos quedarían muchísimas más por mencionar):

SUCESIÓN DE CAUCHY

Una sucesión de Cauchy se caracteriza por poder encontrar un término de una sucesión tal que la distancia entre dos términos de la misma sea tan pequeña como se desee: {xn} es de Cauchy ↔ para todo ε>0 existe no natural tal que |xn-xm|<0.

El interés especial que tienen esta sucesión se debe a que en todo espacio métrico todas la sucesiones de Cauchy son convergentes.

TEOREMA DE CAUCHY

Dadas dos funciones continua f y g en un intervalo cerrado [a,b] y derivable en el abierto (a,b) existe un punto c del intervalo (a,b) tal que: