Suma de Monomios

Para realizar la suma de monomios, nos debemos fijar en los coeficientes y sus acompañantes, las variables (o también conocidos como parte literal, por aquello de que son letras).

Voy a dividir este articulo en dos secciones, primero hablaremos de suma con monomios semejantes y finalmente como proceder en caso de que nos encontremos con monomios no semejantes.

 

a) Suma de monomios semejantes: En este caso, los monomios tienen las variables iguales, con los mismos exponentes, procederemos agrupándolos según su parte literal y sumando normalmente:

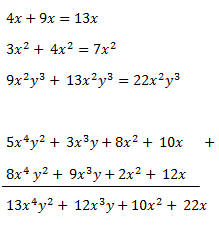
El truco está en agruparlos debidamente como he hecho en el último ejemplo de arriba. Obviamente, la suma de ambos monomios, será otro monomio semejante.

 

b) Suma de Monomios no semejantes: A diferencia de antes, los monomios no semejantes no tienen igual parte literal, por lo que procederemos a simplemente anotar esa suma y dejarla planteada:

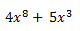
Por tanto, podemos deducir que para poder sumar monomios, hemos de tener obligatoriamente monomios semejantes.

 

La suma de monomios cumple las propiedades:

 

A) Asociativa: Siendo los monomios 3x^2 , 7x^2 y 12x^2 semejantes, se cumple que:

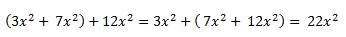
B) Conmutativa: Con dos monomios, 5x^3 y 8x^3 se cumple que:

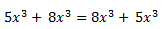
El orden de los sumandos como veis no altera nuestro resultado.

 

C) Elemento neutro: El elemento neutro en el caso de la suma de monomios, es el monomio cero, cuyo valor numérico es cero, es decir, con un monomio cualquiera, axⁿ :

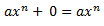
Viene a decir que sumándole ese monomio cero, el resultado es el mismo y no varía.

D) Elemento opuesto: El resultado de cambiar el signo de un monomio es su opuesto, y la suma de estos da como resultado cero:

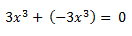
Acordaros de que el opuesto es ese mismo monomio cambiado de signo( si es +, ponéis – y si es – ponéis +).

*Nota*: Si no tiene signo, el signo que lleva implícito es el positivo, así que si no veis el símbolo de más, acordaos de eso.

 

Para terminar, os voy a dejar la forma generalizada de expresar la suma de monomios, que creo se ve mejor:

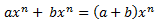
Es decir, la suma de monomios semejantes, al final no es más que sumar los coeficientes que tengan igual parte variable (las incógnitas «x») y los que no la tengan simplemente dejadlos planteados, pues no es posible sumar un cuadrado con un cubo por ejemplo, ya que serían potencias de distinta base.