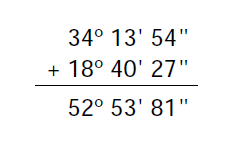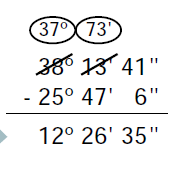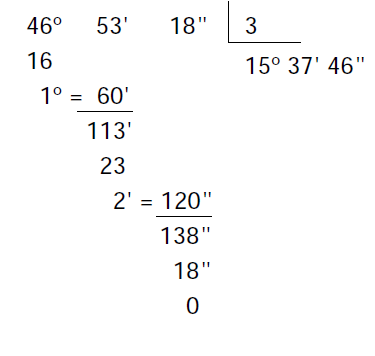Operaciones con ángulos

A lo largo de todo este blog, hemos aprendido a operar con números naturales, números enteros, fracciones, decimales, polinomios….vamos, hemos aprendido ha operar con casi todo lo operable. Ahora le ha llegado el momento a los ángulos.

Recordemos que los ángulos normalmente vendrán expresados en grados(º), minutos(«) y segundos(«»).

SUMA DE ÁNGULOS

Los pasos que debemos llevar a cabo para sumar dos ángulos son:

1º. Colocamos un ángulo debajo de otro, haciendo coincidir segundos con segundos, minutos con minutos y grados con grados, quedando determinadas de esta manera tres columnas.

2º. Sumamos cada uno de las columnas anteriores por separado.

3º. Tenemos que dejar todas las unidades, excepto los grados, con un número menor que 60 (entre 0 y 59). Para ello, comenzando por el final, es decir, por los segundos, en el caso de que sea mayor o igual a 60 dividimos la cantidad entre 60, de tal forma que el cociente será el número de minutos (en este caso, o de la unidad siguiente en cualquier otro)que le sumaremos a los que ya tenemos, y el resto el número de segundos que quedarán. Este proceso se repetirá con los minutos obtenidos si son mayor o igual de 60.

Ejemplo: Realiza la suma de los siguientes ángulos: Â= 34° 13″ 54″ y Ḃ= 18° 40″ 27″.

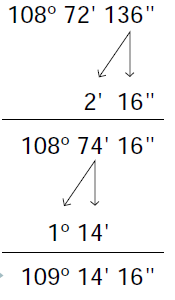
1º y 2º. Colocamos la suma por columnas y sumamos:

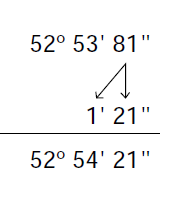
3º. Como nos han salido 81 segundos, dividimos entre 60, 81:60, obtenemos de cociente 1, y de resto 21. Por tanto, sumamos un minuto a los que teníamos antes, (53+1=54″), obteniendo el siguiente resultado:

RESTA DE ÁNGULOS

Los pasos que tenemos que seguir para poder restar ángulos son un poco más complejos:

1º. En primer lugar, igual que en el caso anterior, colocamos nuestro ángulos uno debajo de otro diferenciando en tres columnas.

2º. Una vez colocado, comenzamos a restar, empezando por los segundos. A la hora de restar, podemos encontrarnos con la situación de que el número de arriba sea menor que el de abajo, entonces, para poder hacer la resta, tendremos que quitar una unidad del orden superior (los minutos) y sumarle entonces 60 de tal forma que ya podremos realizar la resta. Este paso, se realizará las veces que sea necesario.

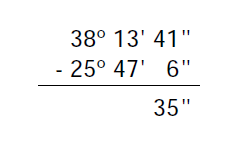
Ejemplo: Dados los siguientes ángulos: Â= 34 = 38° 13″ 41″ y Ḃ = 25° 47″ 6″, realiza la siguiente resta: Â – Ḃ .

1º. Colocamos los ángulos y restamos.

2º. Con los segundos no hay problema, pero a la hora de restar los minutos como 13″ es mayor que 47″, entonces quitamos un minuto al ángulo de tal forma que nos quedan 37º, y 73″:

PRODUCTO DE UN ÁNGULO POR UN NÚMERO NATURAL

Cuando multiplicamos un número por un ángulo seguimos los siguientes pasos:

1º. Multiplicamos cada unidad por el número entero, tanto los grados, minutos y segundos.

2º. Por último, al igual que en la suma, dejamos todas las unidades excepto los grados entre 0 y 59.

Ejemplo: Multiplica el ángulo  = 27° 18″ 34″ por 4.

1º. Multiplicamos cada unidad como hemos indicado:

2º. Pasamos los segundos a minutos, que se añaden a los que tenemos, y por último se cambian los minutos.

DIVISIÓN DE UN ÁNGULO POR UN NÚMERO NATURAL

Cuando dividimos un ángulo por un número entero seguimos los siguientes pasos:

1º. Para dividir el ángulo, al revés que en los casos anteriores, comenzamos dividiendo los grados por el número entero, el resto obtenido, se multiplica por 60 y se pasa a los minutos. Repetimos el mismo proceso con los minutos y por último se dividen los segundos.

Ejemplo: Dividir el ángulo Â=46° 53″ 18″, por el número 3.

1º. Comenzamos dividiendo los minutos: