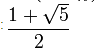Números irracionales
Hace muy poquito estuvimos viendo los números decimales y como podíamos operar con ellos. Además vimos como pasarlos a forma de fracción, tratándose entonces de números racionales. En cambio, había un tipo de números que tenían infinitas cifras decimales y por tanto no se podían escribir como fracción, estos son los números irracionales. Pero no nos confundamos, los números irracionales están dentro de los números reales, aunque este conjunto de números no constituyen una estructura algebraica como en el caso de los naturales o los enteros.
UN POCO DE HISTORIA
El concepto de número irracional tiene sus orígenes en la Escuela Pitagórica, donde se descubrió la existencia de estos números que no eran enteros ni tampoco racionales como fracciones; aunque en un principio se llamaron números inconmensurables.
El origen de estos números puede ser que se deba al problema de resolver la longitud de la diagonal de un cuadrado de lado uno utilizando el Teorema de Pitágoras, siendo el resultado raíz cuadrado de dos: √2; que se considera el ejemplo más claro de los números irracionales.
CLASIFICACIÓN
Podemos clasificar los números irracionales en dos tipos:
– Números algebraicos: Este tipo de números irracionales son los que se obtienen como resultado de alguna ecuación algebraica y que vienen expresados por un número finito de radicales libres o anidados. Todas las raíces de cualquier orden que no son exactas, están dentro de este conjunto.
– Números trascendentes: Por otro lado, cuando no podemos representar el número como radicales libres o anidados, decimos que el número irracionales es trascendente. Estos números se obtienen mediante operaciones que reciben el nombre de funciones trascendentes, las cuales se utilizan en trigonometría, logaritmos, etc. No obstante, también son números trascendentes los que escribimos de forma aleatoria con infinitas cifras decimales.
NÚMEROS IRRACIONALES FAMOSOS
Existen algunos números irracionales que son muy importantes debido a su uso en las operaciones mencionadas anteriormente (funciones trascendentes) como las funciones trigonométricas y logaritmos. Debido a su importancia, estos números se identifican mediante símbolos. Los más importantes son:
– El número Pi (π): Este número nos da la relación existente entre la longitud de una circunferencia (su perímetro) y la longitud de su diámetro. Se utiliza no solo en matemáticas, sino también en física e ingeniería. El valor aproximado de este número, del cual todavía se siguen descubriendo cifras decimales es: 3,141592653589… Para realizar operaciones con él, en la calculadora hay un tecla que lo tiene memorizado, o simplemente redondeamos: 3,14 cuando empezamos a trabajar con él; o 3,1416, dependiendo de la precisión que queramos lograr.
– El número e: Este número fue descubierto por Euler. Su valor aproximado es 2,718281828459… Se utiliza sobre todo en cálculo, por ser el valor del siguiente límite:
– El número áureo (ϕ): También conocido como razón áurea o número de oro, expresa la proporción entre dos segmentos de una recta. Esta proporción ha sido usado a lo largo de la historia por muchos artistas en sus obras, el ejemplo más famoso es la obra de Leonardo Da Vinci conocida como “El hombre de Viturvio”.
Su aproximación es 1,618033988749…. Además es la solución de la ecuación de segundo grado:
cuyo valor es: 
La propiedad más importante característica de estos números es la propiedad cerrada, que quiere decir que cuando operamos con números racionales, sumas, restas, productos, potencias, etc.; se obtiene siempre un número racional. Esta propiedad se cumple siempre salvo en el caso de la radicación.
