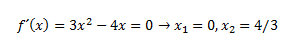Monotonía de una función

Una de las características más importantes a la hora de hacer la representación gráfica de una función es estudiar su monotonía, es decir donde crece y donde decrece nuestra función. Así como determinar los máximos y/o mínimos en el caso de que los tuviera. Además, si todavía tenemos algunas dudas sobre la representación, también podemos estudiar su curvatura y los puntos de inflexión.

Todo eso y mucho más es lo que estudiaremos a continuación.

CRECIMIENTO Y DECRECIMIENTO

Definiciones:

-Diremos que una función es creciente en un intervalo, si para cualesquiera dos puntos de ese intervalo x, y tales que x<y, entonces se cumple que f(x)<f(y).

-Diremos que una función es decreciente en un intervalo, si para cualquiera dos puntos de ese intervalo x, y tales que x<y, entonces se cumple que f(x)<f(y).

Una condición necesaria y suficiente para saber si una función es creciente o decreciente en un punto dado es el estudio del signo de su derivada, de tal forma que podemos decir que:

-Diremos que f es creciente en el punto a si y sólo si su derivada en ese punto es positiva: f´(a)>0.

-Diremos que f es decreciente en el punto a si y sólo si su derivada en ese punto es negativa: f´(a)<0.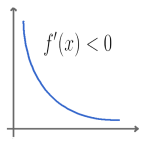

-Diremos que f presenta un punto crítico (un posible máximo o mínimo) cuando la derivada en ese punto sea 0: f´(a)=0.

MÁXIMOS Y MINÍMOS

Definición: Diremos que f tiene un máximo en el punto a si f(a)>f(x) para todo x perteneciente a un entorno de a. Análogamente, diremos que f presenta un mínimo en el punto a si f(a)<f(x) para todo x perteneciente a un entorno de a.

Una condición necesaria para que f presenta un máximo o un mínimo es que la derivada en ese punto sea cero.

¡Pero cuidado! No se cumple el recíproco del anterior, ya que si f´(a)=0, no significa que en el punto a halla un máximo o un mínimo.

CURVATURA Y PUNTOS DE INFLEXIÓN

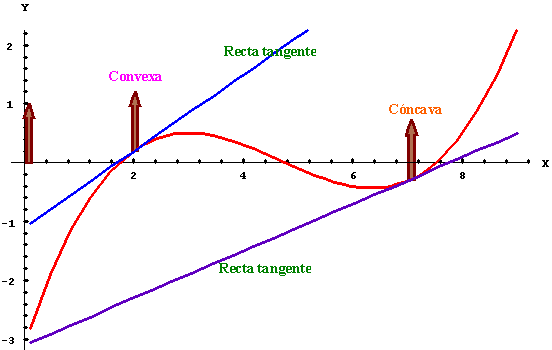
Definición: Diremos que una función es cóncava en un punto, cuando la recta tangente en ese punto queda por debajo de la función. Análogamente diremos que la una función es convexa en un punto, cuando la recta tangente en ese punto queda por encima de la función.

Una condición necesaria y suficiente para estudiar la curvatura de una función es mediante el signo de la segunda derivada:

– Una función es cóncava en un punto a si y sólo si f´´(a)>0

– Una función es convexa en un punto a si y sólo si f´´(a)<0

– Diremos que f presenta un punto de inflexión en a si f´´(a)=0

Hay mucha controversia a la hora de determinar a qué llamamos cóncava y a qué llamamos convexa, pero lo más importante es tener claro cómo sería el dibujo de la función, es decir:

-si f´´(a)>0, es decir, es positiva: +, le hacemos corresponder una cara feliz (sonrisa hacia arriba)

-si f´´(a)<0, es decir, es negativa:-, le corresponde una cara triste (sonrisa hacia abajo)

Vamos a realizar para finalizar un ejemplo en el que diremos los pasos que hay que dar para poder hacer el estudio de la función:

Ejemplo: Estudia la monotonía, los máximos y mínimos (si los tuviera).

En primer lugar, hacemos la derivada y la igualamos a cero.

Elaboramos una tabla, en la que vamos a estudiar el signo de la deriva en los puntos entre medias de las soluciones que nos han dado:

Por tanto en x=0 hay un máximo (0,3) y en x=4/3 hay un mínimo (4/3, 49/27)