Función error
La función error, también denominada como función error de Gauss, es una función que podemos encontrar en distintos campos como: estadística, probabilidad (la famosa campana de Gauss) y las ecuaciones diferenciales parciales (cuyas aplicaciones son tan variopintas como el cálculo de la difusión de la sal en agua). La expresión es la siguiente:
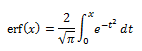
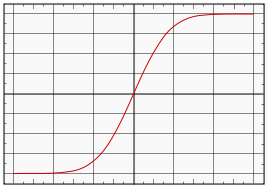
La función error tiene una serie de propiedades y aplicaciones que la hacen especialmente útil en diversas áreas de la matemática y la física. En particular, es de gran utilidad en el análisis de fenómenos que siguen una distribución normal, como la mencionada altura de los varones de una ciudad. Pero, ¿por qué es tan relevante esta función en estos contextos?
La razón principal es que la función error permite calcular de manera exacta las probabilidades asociadas a una variable aleatoria normal, que es una de las distribuciones más comunes en la naturaleza y en los fenómenos sociales. De hecho, la función error es la función de distribución acumulada de una variable aleatoria normal estándar, es decir, una variable normal con media 0 y desviación estándar 1.
Además, la función error tiene una serie de propiedades matemáticas que la hacen fácil de manejar. Por ejemplo, es una función impar, lo que significa que su gráfica es simétrica con respecto al origen. Esto simplifica muchos cálculos, ya que permite reducir el problema de calcular la probabilidad asociada a un intervalo a calcular la probabilidad asociada a un intervalo simétrico con respecto al origen.
Propiedades
1) Es una función impar, es decir, no-simétrica:
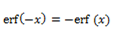
2) Para todo número complejo, se verifica que:
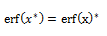
Siendo x* el conjugado de x, es decir:
x= a + bi
x*=a – bi
3) Hay casos, en los que nos encontramos con funciones difíciles de integrar, como e^(-t2), que no se puede hacer de forma directa. En esos casos debemos usar una expansión de la función, por medio de una serie de Taylor, obtendremos, como es lógico, la serie de Taylor de la función error:
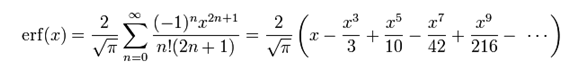
4) Existe una relación simple entre la Función Error y la Función Distribución para una variable aleatoria (con media «μ» y desviación típica «σ»):
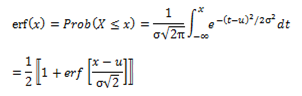
Un uso de esta función, se da cuando, teniendo una distribución normal (desviación típica σ y esperanza 0), entonces:
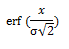
Que es la probabilidad de que el error de una mediación individual se encuentre comprendido en el intervalo –x y +x.
Además, la función error tiene una serie de aplicaciones prácticas interesantes. Por ejemplo, se utiliza en el análisis de experimentos de difusión, donde se mide cómo se dispersa una sustancia en un medio. En estos casos, la función error permite describir la concentración de la sustancia en función del tiempo y la distancia al punto de origen. También se utiliza en el análisis de datos en ciencias sociales y en la industria, donde se utiliza para modelar errores de medición y para analizar la variabilidad de los datos.
En resumen, la función error es una herramienta matemática de gran utilidad en diversas áreas de la ciencia y la ingeniería. Su estudio y comprensión puede abrir la puerta a una mejor comprensión de fenómenos complejos y a la resolución de problemas prácticos.
>>Ejemplo:
Según un estudio, la altura de los varones de cierta ciudad es una variable aleatoria X, que podemos considerar que se distribuye según una Ley Gaussiana de valor esperado μ=175cm y desviación típica σ = 10cm. Dar un intervalo para el que tengamos asegurado que el 50% de los habitantes de la ciudad estén comprendidos en él.
Solución:
Tenemos que
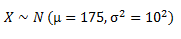
Lo que buscamos es el intervalo que nos asegure que el 50% de los habitantes tengan alturas comprendidas en el. Debemos encontrar un intervalo que esté centrado en la media, y que, además, sea el más pequeño posible (y contenga al mencionado 50% de la muestra).
Como se distribuye según las leyes gaussianas, la probabilidad estará concentrada en su mayor parte en la media. Entonces, tomaremos un intervalo que contenga un 25% de probabilidad del lado izquierdo más próximo a la media y un 25% del lado derecho, quedando una figura así:
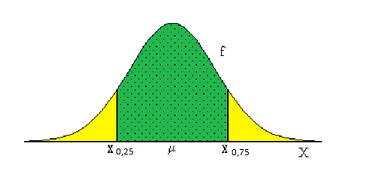
Estos valores se pueden buscar en una tabla de distribución normal, tipificándolos primero, para volver a destipificarlos después
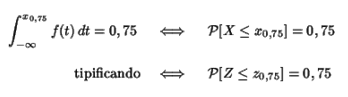
donde
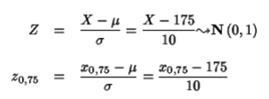
Buscamos el valor en tabla, z0,75 , y se destipifica:
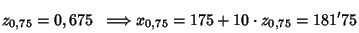
Similarmente se calcularía
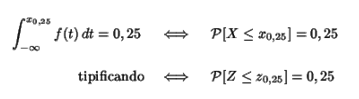
donde
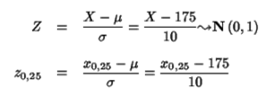
Por la simetría de la distribución normal con respecto al origen, tenemos que z0,25= – z0,75. Entonces:
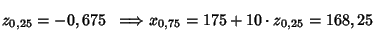
El 50% de la población tiene un peso comprendido en el intervalo [168,25,181,75], que es simétrico respecto a la media, y es el más pequeño de todos los posibles (es más preciso).

