Figuras planas

El estudio de las figuras planas y también sus propiedades geométricas, comprende a todo tipo de polígonos en general, sean regulares o irregulares, como también el círculo. Su estudio comprende las relaciones entre líneas puntos y ángulos de los polígonos irregulares, los métodos para el dibujo de estas figuras y los métodos de cálculo de su superficie. Debemos tener en claro que un polígono irregular es aquel en el cual sus lados no son de igual longitud y que sus vértices no están contenidos dentro de una circunferencia. Mientras tanto un polígono regular es aquel que tiene todos los lados con una misma longitud y que también tiene todos los ángulos interiores de la misma medida. Veremos a continuación cuales son estas figuras planas.

El triángulo

Es una poligonal cerrada con tres lados y tres ángulos, los cuales sumados da 180º. Cada uno de los lados es menor que la suma de los otros dos, entonces a < b + c, b < a + c, c < a + b. con esto podemos deducir quela diferencia de dos lados es menor que el tercero. Veamos ahora un ejemplo:

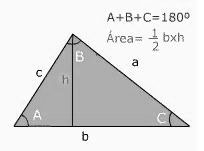
Hay tres clases de triángulos atendiendo a sus lados. Un triángulo equilátero tiene los tres lados iguales, un isósceles tiene dos lados iguales y el tercero desigual, un triángulo escaleno tiene los tres lados desiguales. En cuanto a los ángulos, un triángulo acutángulo tiene sus tres ángulos agudos, un triangulo rectángulo tiene un ángulo recto (90º) un obtusángulo tiene un ángulo obtuso o sea un ángulo mayor a 90º.

El cuadrado

Un cuadrado es una poligonal cerrada de cuatro lados y cuatro ángulos iguales. Cualquier polígono de cuatro lados (cuadrilátero) tiene la condición de que sus cuatro ángulos interiores suman 360º, y cada uno de ellos es un ángulo recto. Como polígono regular se consideran algunas propiedades geométricas de sus líneas y puntos. A continuación vemos lo que es un cuadrado:

El rectángulo

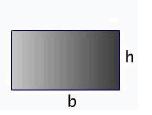
Un rectángulo es también una poligonal cerrada. Todos los angulos interiores de un rectángulo son rectos, pero los lados del rectángulo son iguales paralelamente de a dos, por lo cual podemos decir que un rectángulo es un caso particular de paralelogramo, veamos:

El rombo

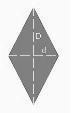
El rombo es un polígono de cuatro lados iguales y paralelos dos a dos, también sus ángulos son iguales dos a dos. Las rectas que unen cada uno de los vértices con el vértice opuesto se llaman diagonales, la mayor de ellas es la diagonal mayor y la menor es la diagonal menor. Si se cortan las dos diagonales en el rombo se forma un ángulo de 90º. Aquí les dejo un ejemplo:

El trapecio

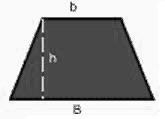
Es un polígono de cuatro lados dos de sus lados son paralelos, la suma de sus ángulos es de 360º. Los lados paralelos se llaman base mayor (B) y base menor (B). Un trapecio es isósceles si sus lados no paralelos son iguales, si esto es así dos de sus ángulos interiores serán agudos y los otros dos obtusos. Un trapecio será rectángulo si uno de los lados que no es paralelo es perpendicular a los paralelos, siendo así tendrá dos ángulos rectos uno obtuso y uno agudo. Como último punto diremos que un trapecio es escaleno si no es rectángulo ni isósceles.

El paralelogramo

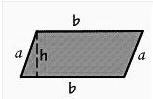
Este un polígono de cuatro lados paralelos dos a dos, también sus ángulos son iguales dos a dos y suman los cuatro 360º. Algunos casos particulares de paralelogramos son el cuadrado, el rectángulo y el rombo. La figura que mostramos a continuación es un romboide, el cual es el caso general de paralelogramo.

Polígonos regulares

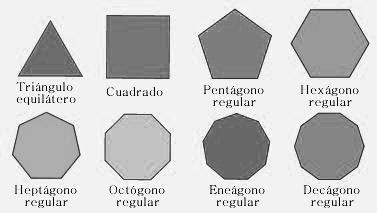
Un polígono regular es aquel que como ya dijimos tiene sus ángulos interiores y sus lados iguales. Veamos a continuación cuales serían:

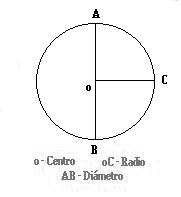
El círculo

El círculo es una figura plana que está delimitada por la circunferencia. A los efectos geométricos equivale a un polígono regular que tiene infinitos lados. En el círculo se consideran las propiedades geométricas de las siguientes líneas y puntos, tales como la circunferencia, el centro que es el punto en el cual equidistan todos los puntos de la circunferencia o el radio, que corresponde a la medida de distancia entre el centro y la circunferencia. También hay otras propiedades tales como el diámetro, la secante, la tangente, el arco la flecha y el sector.