Diagonal principal

En álgebra lineal (rama de las matemáticas que se encarga de estudiar los conceptos tales como vectores, matrices, sistemas de ecuaciones lineales, espacios vectoriales, y transformaciones lineales) una matriz es un conjunto de elementos que en general, suelen ser números ordenados en filas y columnas. Llamamos matriz de orden «m × n» a un conjunto rectangular de elementos que se ordenan en m filas y en n columnas. El orden de una matriz también se llama dimensión o tamaño, siendo m y n números naturales. Las matrices se indican con letras mayúsculas, mientras que los elementos de las mismas con letras minúsculas.

Una matriz cuadrada es aquella que tiene el mismo número de filas que de columnas. Se dice que una matriz cuadrada n ´ n es de orden n y se denomina matriz n-cuadrada. Veamos un ejemplo:

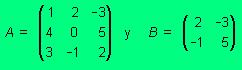
Si una matriz tiene m filas y n columnas, entonces la matriz es de orden m x n. A y B son matrices cuadradas de orden 3 y 2 respectivamente.

La Diagonal principal de una matriz cuadrada es la diagonal que va desde la esquina superior izquierda hasta la esquina inferior derecha. Podemos observar esto en la matriz que sigue a continuación:

A una matriz como la anterior, en la cual solo los elementos de la diagonal principal no corresponden a cero, la denominamos matriz diagonal. La suma de los elementos de la diagonal principal de una matriz se define como la traza de dicha matriz. Podemos apreciar entonces que una matriz diagonal es a la vez una matriz cuadrada en la cual las entradas son todas nulas salvo en la diagonal principal.