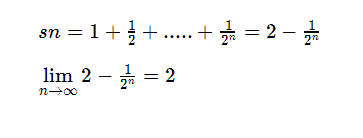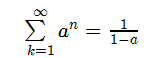Convergencia de series

Hoy vamos a estudiar la convergencia de series numéricas, dando algunos de los criterios que se utilizan para determinar cuando es una serie convergente. En primer lugar daremos unas definiciones previas a modo de introducción del tema.

DEFINICIONES

-A partir de la sucesión de números reales (an), consideraremos una nueva sucesión (sn) que definimos como la suma de sus términos de la siguiente manera: s1=a1, s2=a1+a2, es decir: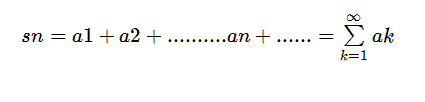

Esta sucesión se denomina sucesión de sumas parciales de la sucesión (an), y cuando n es infinito, ∑an con 1 ≤n≤∞ recibe el nombre de serie asociada la sucesión (an).

-Se dice que una serie es convergente cuando el límite de la sucesión da un número real, lim sn=s cuando n tiende a infinito. En este caso diremos que la serie anterior converge a s.

-En caso contrario, cuando el valor del límite es infinito, la serie será divergente.

-Cuando el límite varía, dando en algunas ocasiones valores positivos y en otras valores negativos, diremos que la series es oscilante.

Ejemplo 1:La serie ∑(1/2)^n es una serie convergente ya que si realizamos la serie de las sumas parciales tenemos:

Por tanto la serie converge a 2.

Ejemplo 2: La serie ∑1 es divergente por el límite de la sucesión de las sumas parciales tiende a +∞.

Ejemplo 3: La serie ∑(-1)^n es una serie oscilante, ya que dependiendo de la paridad de n la sucesión de las sumas parciales nos da un resultado distinto: -1 cuando n es impar y 0 cuando n es par.

CRITERIOS DE CONVERGENCIA DEPENDIENDO DEL TIPO DE SERIE

-Cuando trabajos con una serie geométrica, que recordamos es de la forma ∑a^n donde a es una constante real, diremos que es convergente si y sólo si |a|<1, y en esta caso, el valor de su suma es:

En caso contrario, |a|>1, la serie es divergente.

-Si la serie es de tipo armónico, que recordamos era de la forma ∑1/n^a, donde a es una constante real; la convergencia en este caso depende del valor de a. Si a>1 la serie será convergente y si a≤1 será divergente.

-En último lugar, cuando tenemos una serie aritmético-geométrica, que son de la forma ∑P(n)a^n, donde P(n) es un polinomio de grado mayor o igual que uno (de donde viene la parte aritmética de la serie) y a es una constante real (a^n, evidentemente, es la parte geométrica), entonces, será convergente si y sólo si |a|<1.

Ejemplo 1: La serie ∑(1/2)^n es convergente, ya que es una serie geométrica, donde a=1/2 y como |1/2| <1, entonces es convergente.

Ejemplo 2: La serie ∑1/n^0,5 es una serie armónica, donde a=0,5, por tanto como a≤1, entonces será divergente.

Ejemplo 3: La serie ∑(n-1)/2^n es una seria armónico-geométrica, donde a=1/2, por tanto la serie es convergente.

PROPIEDADES ALGEBRAICAS

Dadas dos series convergentes ∑an=a´ y ∑bn=b´, entonces:

1. La suma de ambas series es convergente y además converge a la suma de a´+ b´: ∑(an+bn) = ∑an + ∑bn = a´ + b´

2. Si multiplicamos una serie convergente por una constante real, k, la serie resultante también es convergente, además converge al producto de ka´: ∑kan = k∑an = ka´