Coeficiente binomial

Los coeficientes binomiales también llamados números binomiales o combinaciones son una serie de números estudiados en combinatoria que indican la cantidad de modos en que se pueden extraer subconjuntos a partir de un conjunto dado. Pese a esto, dependiendo del punto de vista que tenga la exposición, se suelen utilizar diferentes definiciones.

Si n es un número entero positivo y multiplicamos (x+y)n término por término, serán estos el producto de las x y las y, donde una x o una y venga de cada uno de los factores x+y. Por ejemplo lo siguiente:

Produce términos de la forma:

Y sus coeficientes son: 1, 3, 3, y 1.

El coeficiente de xy elevado a 2, por ejemplo, es (3/2)=3 el numero de formas en que podemos seleccionar los dos factores que suministran las y. Entonces el coeficiente x elevado a y 2 multiplicado por y, es (3/1)=3 el número de formas en que podemos seleccionar el factor que proporciona las y, y los coeficientes de x elevado a 3 e y elevada a 3 son: (3/0)=(3/3)=1

De forma mas general podemos decir que si n es un entero positivo y multiplicamos (x+y) elevado a n, término por término, el coeficiente entonces de:

sería (n/r) El numero de formas en la que podemos elegir los r factores que facilitan las y. A razón de esto nos referimos a( n/r) como un coeficiente binomial.

Podemos enunciar entonces los siguientes teoremas:

El teorema uno sería :

Sirve para cualquier entero positivo n. El calculo de coeficiente binomial puede simplificarse por medio del uso de Los teoremas a continuación.

El teorema dos:

dos enteros negativos n y r n ≥ r se verifica la siguiente igualdad :

Podemos decir también que cuando elegimos un subconjunto de r objetos de un conjunto de n objetos diferentes estamos dejamos un subconjunto de n-r objetos y como resultado hay muchas formas de elegir r objetos como dejar (o seleccionar) n-r objetos. Para manifestar y demostrar el teorema en forma algebraica, escribimos lo siguiente:

Por Ejemplo:

Determinemos .(20/12) y (17/10)

Para obtener (20/12) utilizamos el hecho de que (20/12)=(20/8), buscamos (20/8)=125,970 y de la misma forma .(17/7)=19,448

Teorema 3: Para cualquier número entero positivo n y para r= 1,2,…,n-1, verificamos lo siguiente:

El coeficiente binomial es muy utilizado en el Triângulo de Pascal, donde el término en la línea n y columna k es :

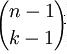
n representa el número de la línea (posición vertical) mientras que k representa el número de la columna (posición horizontal). Para formarlo se suman los números del renglón de arriba que luego se colocan en el siguiente. Cuando un binomio es elevado a una cierta potencia los números encontrados son los coeficientes de los términos.

………………1
…………..1…….1.
………….1…2………1
………1..3……3……..1
……1….4…6……..4…..1
…1….5…10–10…..5…..1

Podemos decir que el triángulo de Pascal es un conjunto infinito de números enteros ordenados en forma de triángulo que expresan coeficientes binomiales. El interés del Triángulo de Pascal se debe a su aplicación en álgebra lo cual permite calcular de forma simple los números combinatorios y con esto aplicarlo a el binomio de Newton. Dicho binomio es una expresión algebraica que se forma por dos términos separados, como x + y. El teorema del binomio nos dice que la expresión general de un binomio, como podría ser(x + y), elevado a la n-ésima potencia se da por una ecuación. El desarrollo completo de esto contiene n + 1 términos, comenzando con el término cero y terminando con el término n-ésimo. Aquí el término cero sería xn.

Además de su aplicación en el binomio de Newton, los coeficientes binomiales también se utilizan en la expansión de polinomios multinomiales, en la definición de polinomios de Bernstein, en la definición de las funciones de B-spline, en la generación de números de Fibonacci, entre otros.

En la teoría de grafos, los coeficientes binomiales juegan un papel importante en el conteo de subgrafos y en la determinación de la cantidad de caminos entre dos nodos. En la teoría de códigos, se utilizan para determinar la cantidad de códigos posibles y su capacidad de corrección de errores.

En estadística, los coeficientes binomiales son fundamentales en la definición de la distribución binomial, que describe la cantidad de éxitos en una serie de ensayos independientes de Bernoulli.

En resumen, los coeficientes binomiales son una herramienta matemática fundamental con una amplia gama de aplicaciones en diversas disciplinas. Su estudio y comprensión son esenciales para cualquier estudiante o profesional de las matemáticas, la física, la informática, la estadística y otras áreas relacionadas.