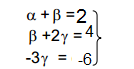Base de un espacio vectorial

En el artículo de hoy vamos a estudiar un concepto que se puede considerar el cimiento para el estudio de las rectas y los planos en el espacio. Ya que las coordenadas de los puntos siempre vienen dadas en un determinado sistema de referencia formado por un punto y los vectores de su base.

Definiremos el concepto de base, los pasos que hay que seguir para determinar que un subconjunto es una base y como podemos hallar su dimensión.

Definición: Un subconjunto finito de vectores se llama base si los vectores que lo forman son linealmente independientes y forman un sistema generador del espacio.

Un sistema generador del espacio Rn es un subconjunto A={v1,v2,v3,…vn} tal que todo vector del espacio puede ser expresado como combinación lineal de elemento de A, es decir, para todo u de Rn, u se puede escribir como: u = a1∙v1+ a2∙v2+….+ an∙vn con a1, a2,…., an número reales donde no todos son cero. Los escalares a1,a2,…, an reciben el nombre de coordenadas del vector u en la base formada por los vectores {v1,v2,….vn}.

Observación: Existen infinitas bases para un mismo espacio.

Ejemplo 1: Demostrar que una base para el plano, es decir, para el espacio R2, es: B={(1,0), (0,1)}.

1º. En primer lugar, tenemos que demostrar que los vectores son linealmente independientes, para ello, como ya hemos visto en ocasiones anteriores, podemos utilizar dos métodos:

Método A: Comprobar que el rango de la matriz que forman es 2, lo cual es evidente.

Método B: Se tiene que cumplir que: a∙(1,0)+b∙(0,1) = (0,0) entonces a=b=0, que en este caso también es evidente.

2º. Demostrar que cualquier vector se puede escribir como combinación lineal de los vectores que forman la base, por ejemplo, cojamos el vector (-2,6): a∙(1,0)+b∙(0,1)=(-2,6)→a=-2, b=6. Por tanto las coordenadas en la base B del vector son (-2, 6), en este caso coinciden ya que B es una base especial.

Por tanto B={(1,0), (0,1)} es una base, esta base recibe el nombre de base canónica y es la base que utilizamos siempre que trabajamos en el plano. De forma análoga, la base canónica en el espacio tridimensional será B={(1,0,0), (0,1,0), (0,0,1)}.

Definición: Llamamos dimensión al número de vectores que forman una base. Todas las bases de un mismo espacio tienen la misma dimensión. Es decir, la dimensión de un espacio es el número máximo de vectores linealmente independiente que forman un sistema generador del espacio. Por tanto, también podemos decir que es el máximo rango que puede tener un conjunto de vectores de ese espacio.

Vamos ahora un ejemplo que no sea tan sencillo como la base canónica y donde podamos apreciar los pasos que hay que hacer para comprobar que un subconjunto de vectores es una base.

Ejemplo 2: Comprueba si el siguiente subconjunto de vectores es una base y calcula su dimensión, B={(1,0,0), (1,1,0), (0,2,-3)}.

a) En primer lugar comprobamos que es base siguiendo los mismo pasos que en ejemplo anterior:

1º) Comprobar que los vectores son linealmente independientes. Utilizando el primer método, comprobamos que forman una matriz de rango 3.

2º) Comprobamos que forman un sistema generador, por ejemplo si consideramos el vector (2,4,-6):

(2,4,-6)=α∙(1,0.0)+β∙(1,1,0) + γ∙(0,2,-3), obtenemos el siguiente sistema:

Que es un sistema compatible determinado, de la última ecuación obtenemos que γ=2, sustituyendo en la segunda obtenemos el valor de β=0, y por último α=2.

b) La dimensión de la base, como hemos dicho coincide con el número de vectores que la forman, por tanto dim(B)=3.