Asíntotas oblicuas
Podemos definir el concepto de asíntota de la siguiente forma:
Dada una función Y = f(X) cuya gráfica es una curva C decimos que la recta “r” es una asíntota de f (X) cuando la curva C se acerca mas y mas a “r” indefinidamente sin llegar a coincidir nunca con la propia “r”.
Sabiendo esto podemos decir que una asíntota es una recta. Se distinguen tres tipos de asíntotas que son las asíntotas horizontales, asíntotas verticales y asíntotas oblicuas.
Las asíntotas oblicuas de una función son rectas oblicuas de la forma Y= mx + n
Una función racional tiene asíntotas oblicuas si el grado del numerador es mayor que el grado del denominador.
Pueden encontrarse en una función hasta dos asíntotas oblicuas distintas. Una por la derecha de su gráfica y otra por la izquierda. Podemos calcular esto de la siguiente forma:
![]()
Si m me da distinto de cero y ± ∞ podemos calcular n de esta manera:
![]()
Si n nos da como resultado un número infinito, entonces la recta Y = mx + n será una asíntota oblicua para f (x) por el lado izquierdo.
Para el lado derecho podemos proceder de la siguiente forma, partiendo de lo siguiente:
![]()
En este caso, si m da un resultado distinto de cero y ± ∞, calcularemos n de esta forma:
![]()
Si el resultado de n es un número real, entonces la recta Y =mx +n será una asíntota oblicua para f(x) por el lado derecho.
Es posible que nos encontremos con funciones que no tengan asíntotas oblicuas. Que tengan una asíntota oblicua por ambos lados. Que tengan una asíntota por un lado nada más, o que tengan dos asíntotas oblicuas diferentes.
Veamos un ejemplo de asíntotas oblicuas.
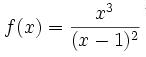
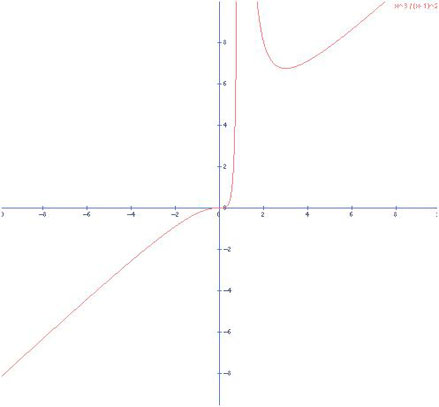
Esta función posee una asíntota oblicua. Si los siguientes Límites existen y son finitos diremos que existe una asíntota oblicua y que la ecuación de la recta está dada por: y=mx+b
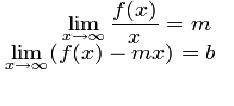
Un buen truco para saber de antemano si tenemos una asíntota oblicua es observar si se trata de una fracción. De ser así, solo tenemos una asíntota oblicua si el numerador posee un grado mayor que el denominador.
También tengamos en cuenta que una función no puede tener una asíntota horizontal y otra oblicua por el mismo lado. Pero si una horizontal por un lado y una oblicua por el otro.

